Understanding SVM

Based on Andrew Ng’s Machine Learning Basic.

SVM is a kind of optimization of Linear Regression.

In Linear Regression, we trying to minimize the error function:

in the function above, $-\log h_\theta(x^{(i)})$ and $-\log (1 - h_\theta(x^{(i)}))$ are called cost function, which used to measure the distant between prediction result and actual result.

Because we use sigmoid function for you prediction, so the curve of $-\log h_\theta(x^{(i)})$ looks like this:

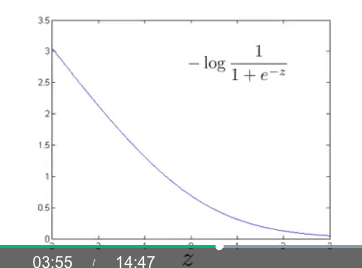
We use a two linear function to describe that curve roughly:

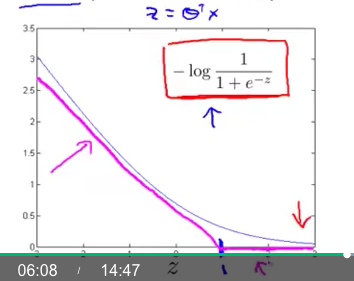
And we call this new cost function $ Cost_0(\theta^Tx)$

According to the cost function $Cost_0(\theta^Tx)$, if we want to minimize the it, we should have $\theta^Tx \ge 1$

(in the case of the result $y = 1$)

(Minimizing the cost function $Cost_0(\theta^Tx)$ will minimize the Error function $\xi$ too)

So we can get a important restriction: \(\theta^Tx \ge 1\)

This restriction makes the data points the boundary have the influence of angle of the linear boundary. In other words, which means we can have a margin for the boundary. We are trying to finde the biggest margin of the boundary.

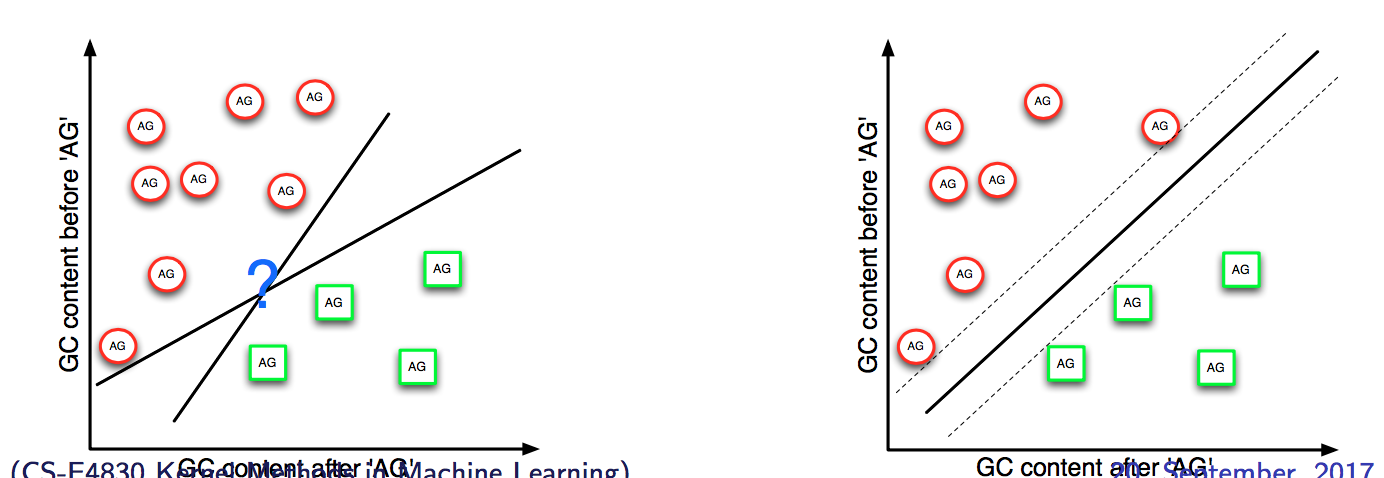
How to modify the margin?

From my understanding, we can rewrite the restriction as this:

Where the $\pmb x’$ is the projection of $\pmb x$ on the direction of $\pmb \theta $, $\pmb x = \Vert x \Vert * cos\beta$

norm symbol in Latex: https://tex.stackexchange.com/questions/107186/how-to-write-norm-which-adjusts-its-size

So we have

The factor $C$ will influence the angle theta.

The key step is using a discrete function to replace a continous function, which made the $C \ne 0$

Somewords of Kernel Methods

The course of Andrew Ng is good!

I have been confused what is Kernel and how to understanding the Kernel in a more intuitive way. Before I studying his course I always need to recall a lot of conceptions and try to remember it in a hard way.

The example of him is to describe the Kernel function as a tool of checking the similarity of two points.

So who is our standard? The answer is quite simple but it costs me some time to realize it. Training set is our standard for comparing the similarity. In Andrew’s course, he called it as “landmark”.

When a new data from Testing set comes in, we will use Kernel function to check if the new data similar with each “landmark”. As the result of comparing, it will save the result in a column vector.

As for the whole data set, we can derive a matrix from Testing set, which is called Kernel Matrix.

The size of Kernel Matrix:

Suppose that we have a training set $X_{training} \in R^{m_1 \times n}$, where $m_1$ is the number of data, $n$ is the number of features, or dimesions. The test data set is $X_{testing} \in R^{m_2 \times n}$

So for the Kernel Matrix: $K \in R^{m_1 \times m_2}$

The Kernel function is a projection of a data set, from which we can project the data to a feature space, in that space we can use Linear classifier for classification problem.

Combination of SVM and Kernel Method

They are two seperated things, SVM is a classfier that have better performance than normal linear classifier.

Kernel is a good method that will reduce the computation complex when implementing the classifier.

For my understanding, SVM is a engine in a car and Kernel is the N2O Booster.