Quality Assurance Note 2 - Time automata
这里是关于Quality Assurance课程的第二篇整理笔记
##简介##
Time automata是用于描述系统结构的另一种方法, 和上一篇中提到的Kripke Structure相似.
当我们在使用Kripke Structure 试图描述一个系统的时候, 我们会发现一个问题: Kripke Structure 怎么描述带有时序的系统呢?
所以我们引入了一个时序变量, 使得状态机能够表达时间的顺序.
这就是今天要说的Time Automata.
##Definition of Time Automata##
Timed Automata, extend finite automata with clocks and clock conditions
- Clocks run continuously (they do not stop)
- All clocks run with the same speed (synchronous and uniform)
- Clocks may be reset to zero (at transitions)
- Clocks may affect which transitions can fire (clock conditions)
- Clock domain: positive real numbers and zero \((\Re^+ \cup {0})\)
一般来说, 我们用单个小写字母来表示时钟, 例如 x, y, z.
举个例子!
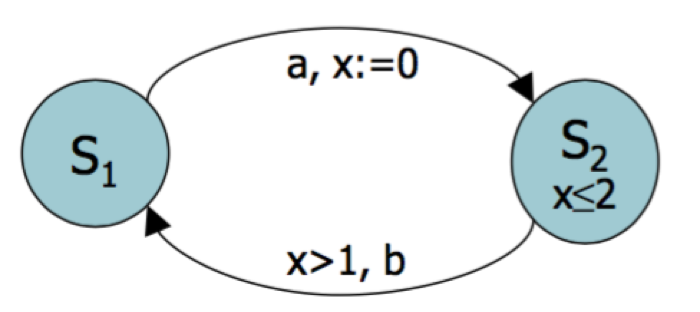
上面这个图中有两个状态, 在这两个状态之间通过transition连接, 每个状态也有labeling function来表示他们自己 (\( S_1,S_2 \), 注意不是 \(x \leq 2\), 因为x在这里只是时钟变量, 并不是表达一个状态的labeling function).
如果只看这三个部分的话, 这张图和普通的Kripke Structure没有任何区别
但是请注意我们这张图上又添加了了一些元素, 例如 \( x:= 0, x > 1, x \leq 2\)之类的, 下面就让我们说说这些是什么
-
在transition上面的表达式(x>1, x:=0), 我们称作guard(转换条件), 它的解释是
Transitions can only fire if the current clock values satisfy the guard (guards enable progress)
这里的fire 意思是”发生”
-
写在状态上面的表达式 (\(x \leq 2\)), 我们称作invariant
The automaton can only stay in a state as long as the invariant is true (invariants ensure progress)
所以一个time automata应该是这样的:

还有许多关于这个图的语义描述和语法描述我就不写下来了, 这种概念的东西背背就好
##Networks of Timed Automata##
涉及到时序的问题的话就会涉及到系统间的消息的传输问题, 就有了同步和异步的概念.
在time automata里面的消息传输有两种方式, 一种是双边同步(Binary Synchronization), 第二种是广播同步(Broadcast Synchronization).
双边同步
一方为发送方, 另一方为接收方, 他们两者都是阻塞的. 意思就是只要有一方没有准备好, 另一方就会一直等待.
广播同步
一方为发送方, 接收方可以有多个. 接收方式阻塞的, 它们会一直等待消息的到来, 但是发送方是非阻塞的, 一旦发送了消息, 它就会直接进行下一步动作
Region and Zones
Time automata十分好用, 因为它更加接近现实生活.
但是问题来了, 计算机是一个有限的状态机的集合, 但是time automata是一个无限状态机. (因为从0秒到1秒之间是可以分成无限个时间片段, 现实世界是连续的模拟量!)
我们的解决方案就是把无限的状态机用一个固定的量程切分, 就像尺子把一段距离切分成许多毫米组成的片段一样.
这里我们使用的量程是1秒.
比如这个例子:
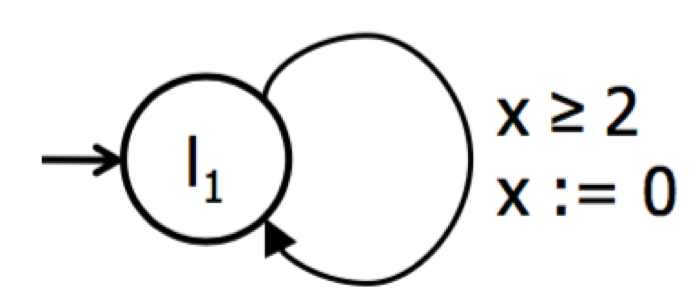
时钟是x. 让我们用秒做单位进行切割
- \( x = 0\)
- \( 0 < x < 1\)
- \( x = 1\)
- \( 1 < x < 2\)
- \( x = 2\)
- \( 2 < x <3\)
- ….
其实从x>2之后我们就没必要再写了, 因为当 \(x \geq 2\) 的时候x又会被\(x:=0\)赋值成为0.
根据我们分割的结果, 我们就可以画出这样的有限状态机
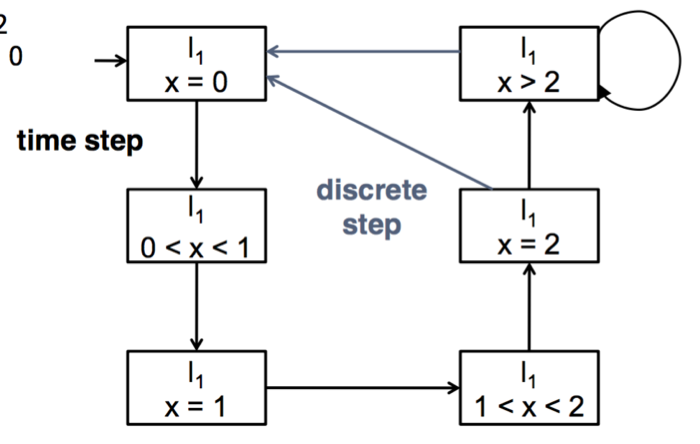
有没有发现现在的图形就很像是最开始提到的Kripke Structure, 这就是Region操作的意义, 把复杂的Time automata转变为简单的Kripke Structure, 从而使得计算机可以运算.
另外!
上面的图形其实有很多冗余的部分, 比如x=0, 0<x<1, x=1, 1<x<2 这4部分都可以合并在一起, 成为一个状态.
于是我们就像下图一样把一样的地方圈出来!
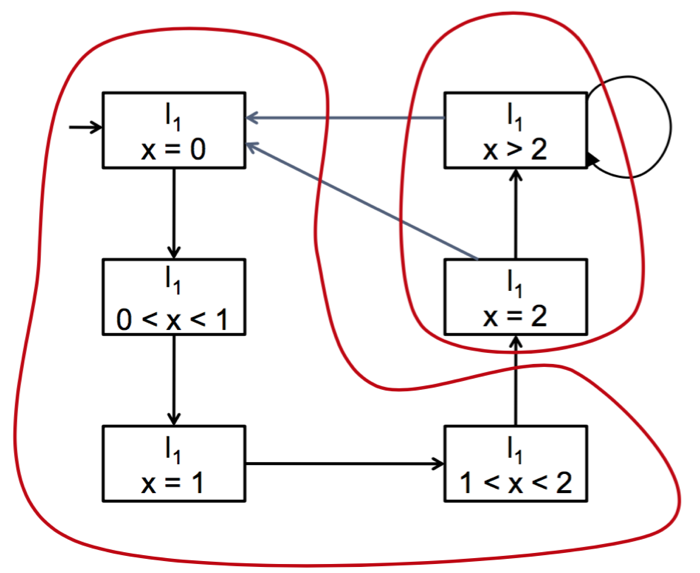
最后得到的结果是这样!
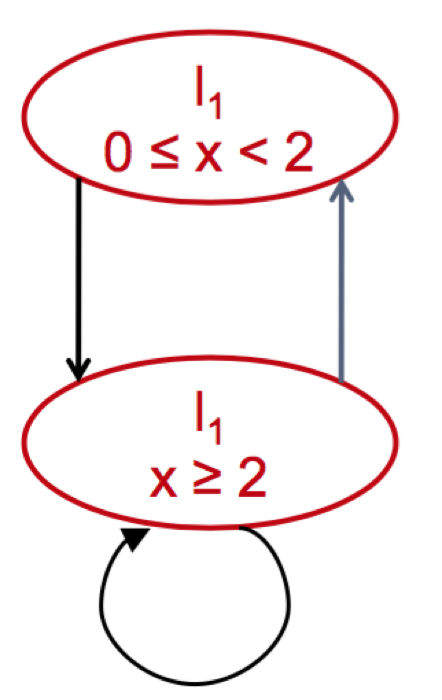
到此为止, Time Automata就彻底变成Kripke Structure的一部分啦!
总结
这个部分主要讲的是怎么用Timed automata来描述一个系统并如何把time automata转变成普通的Kripke Structure.
就这样!